| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 기계학습
- Unsupervised learning
- coding test
- 코딩테스트
- Class activation map
- Machine Learning
- AI
- 설명가능한
- 딥러닝
- Artificial Intelligence
- Interpretability
- Explainable AI
- keras
- 설명가능한 인공지능
- 백준
- SmoothGrad
- 코딩 테스트
- 인공지능
- xai
- grad-cam
- Score-CAM
- python
- meta-learning
- Cam
- GAN
- 메타러닝
- cs231n
- 시계열 분석
- 머신러닝
- Deep learning
- Today
- Total
iMTE
Neural Networks Part 2: Setting up the Data and the Loss 본문
Neural Networks Part 2: Setting up the Data and the Loss
Wonju Seo 2019. 3. 2. 10:59Reference:
http://cs231n.github.io/neural-networks-2/
http://aikorea.org/cs231n/neural-networks-2-kr/
Setting up the data and the model
Neural network는 dot product와 non-linearity 연산을 sequentially 수행한다. Neural networks의 모델은 linear mapping을 non-linear transformation에 적용하는 과정이 연속적으로 진행한다. 이번 장에서는 data preprocessing, weight initialization, loss function을 다룬다.
Data preprocessing
데이터 행렬 X에 대해서 3가지 전처리 방버이 사용될 수 있다.
1) Mean subtraction: 모든 feature (즉 입력)에 대해서 평균값 만큼 차감하는 방법으로 데이터의 중심을 원점으로 이동시키는 transition transformation에 해당한다.
2) Normalization: 각 차원의 데이터가 동일한 범위내의 값을 갖도록 하는 전처리 방법이다. (1) 각 데이터값을 평균 만큼 차감하고 표준 편차로 나눈다. (2) Minmax scaling을 사용하여 최소 최대 값이 0~1 혹은 -1/1을 갖도록 정규화 한다. 이런 방법은 scale이 다른 feature가 동일한 범위를 갖게됨으로써 "동일한 비중"으로 학습에 영향에 미친다는 가정하에 사용된다.
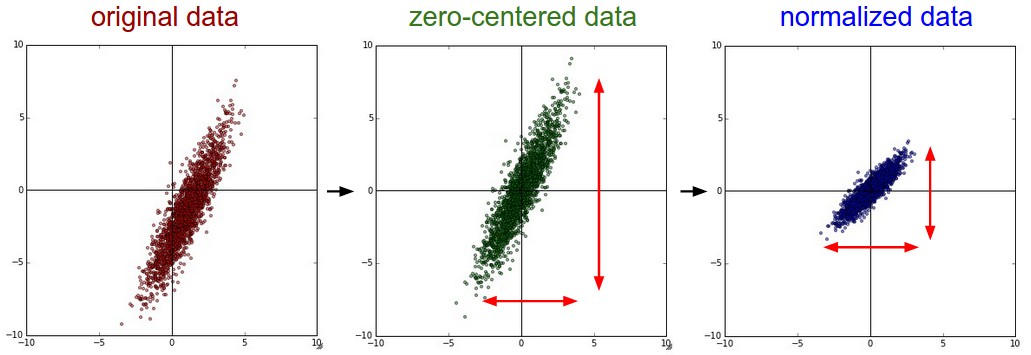
3) PCA와 whitening: mean subtraction을 사용해서 데이터를 정규화한 다음, 데이터 간의 상관관계를 나타내는 covariance matrix를 계산한다. Covariance matrix에서 (i,j) 값은 데이터의 i 번째, j 번째 데이터 간의 covariance를 나타내는 값이다. 그고, 대각선 상의 성분들 (diagonal)은 각 데이터의 성분의 variance와 같다. Covariance matrix는 symmetric, positive semi-definite 성질을 갖고 있어, Singular Value Decomposition (SVD)를 진행할 수 있다.
SVD의 결과로, 구해지는 eigen vector로, 데이터의 차원을 축소할 수 있다. 보통 variance가 큰 차원을 중심으로 축소를 하는 것이 좋은 성능을 유도할 수 있을 뿐만아니라, 데이터를 축소하였으므로 메모리 용량에서 이득을 본다.
Whitening은 eigenbasis data를 eigenvalue값으로 나누어 정규화 하는 기법이다. (Exaggeration noise, 분모가 0이 되는 것을 방지하기 위한 임의의 작은 상수로 인해서 variance가 낮아 noise로 해석이 가능한 데이터까지 포함되어 noise가 과장되는 현상이 나타난다. 이런 경우 보통 큰 수를 분모에 더하는 방식으로 smoothing효과를 추가하여 exaggeration noise를 해결할 수 있다.)
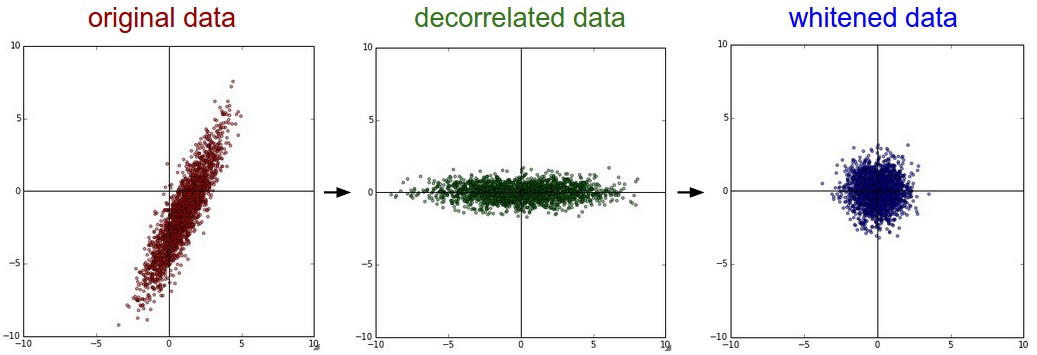
보통, mean subtraction으로 zero-centered data로 변환하거나, 각 데이터를 normalization하는 방법이 일반적으로 사용되는 preprocessing method 이다.
그리고, preprocessing 할 때, training data로 얻은 mean, variance를 갖고 test data에 적용해서 normalization을 진행해야한다. 이는 information leak를 방지한다.
Weight initialization
Neural networks를 학습하기 전에 parameter를 초기화하는 작업은 매우 중요하다. (Gradient descent에서 시작점은 minima에 얼마나 빠르게 도달할 지를 결정하는 중요한 요소이다.)
1) 0으로 초기화 하기: Data normalization기법을 기반으로 weight의 절반은 양의 수, 나머지 절반은 음의 수를 갖는다고 가정할 수 있다. 그래서 더 나아가서 weight을 0으로 초기화 할 수 있다. (평균은 0이니까) 하지만 이 방법은 neurons이 동일한 연산 결과를 초래하고 backpropagation에서 동일한 gradient값을 얻게되어 결과적으로 parameter가 동일한 값으로 update 됨으로, neurons의 asymmetry를 야기할 요소가 사라진다. (만약 bias 가 0이고, weight도 0인데, activation function으로 relu가 사용되면, 모든 neuron은 죽은 상태가 되어 학습이 되지 않는다.)
2) 0에 가까운 작은 난수, weight은 0에 가까운 값이 되어야하고, 0이면 안된다. 0에 가까운 값으로 초기화 하는 방법을 symmetry breaking이라고 한다. 모든 weights들을 난수를 이용하여 고유한 값으로 초기화 함으로써 각 parameter 값이 서로 다른 값의로 업데이트 되어 서로 다른 특성을 학습하도록 하는 것이다. (이렇게 되면, 각 neuron들이 서로 다른 feature를 배우고, 이 feature가 조합되어 더 나은 feature를 만들어내어 결과적으로 성능이 향상된다.)
보통, numpy 함수를 사용해서 weight initialization을 하는데, W= 0.01 * np.random.randn(D,H)로, np.random.randn은 평균이 0, 표준편차가 1인 normal distribution으로 부터 sampling한다. 이 공식으로, 서로 다른 weight은 연관없이 무작위적인 방향성을 갖는다. Normal distribution외에도, uniform distribution을 사용할 수 있으나, 영향은 미미하다.
weight을 0에 가까운 작은 값으로 초기화 하는 경우, backpropagation 연산 과정에서 gradient가 작은 값을 갖게 되어, 역으로 전파되는 gradient 값을 줄여 training에 문제를 일으킨다.
3) 분산 보정, 1/sqrt(n): random으로 초기화된 weight으로 인한 neuron의 출력의 variance는 입력 데이터 수에 비례하여 분산이 커지는 문제점을 갖고 있다. (즉, 입력이 1000이라면, 0.01 * 1000 = 10 정도의 variance를 갖게 되는 것이고, 이는 매우 큰 variance로 network 안에 sigmoid function 혹은 tanh 를 사용한다면, saturation이 되는 문제를 일으킴으로 학습을 방해한다.) 따라서, 입력되는 데이터의 수의 제곱근으로 나누는 연산을 통해서 neuron의 출력의 variance를 1로 정규화 할 수 있다. w=np.random.randn(n)/sqrt(n)
(두가지 type의 weight initialization 방법이 있는데, 보통 S자형과 ReLU에 해당하는 activation function을 기준으로 구분한다. S자형 은 Glorot initialization (e.g., Xavier initialization)을 사용하고, ReLU는 He initialization을 사용한다.)
Glorot initialization
n_in : 이전 layer의 출력 수, n_out : 현재 layer의 출력 수
He initialization
n_in과 n_out이 같으면 Glorot initialization은 var(w)=1/n이지만, He initialization은 var(w)에 2배정도를 곱해준 값으로 ReLU를 activation function으로 갖는 neuron의 weight을 initialization하는 것을 권장한다.
4) Sparse initialization: weight matrix를 0으로 초기화 하고, symmetric한 성질을 깨기 위해서 모든 neuron을 고정된 숫자 아래 단계 neuron들과 무작위로 연결한다.
5) bias 초기화: weight에 random한 값을 설정함으로 대칭성 문제는 해결되기 때문에 bias는 0으로 초기화 한다. ReLU의 경우 bias를 0이 아닌 0.01과 같은 값으로 정하는데, 이는 Dead ReLU를 방지하기 때문이다. (f(x)=max(0,x)) (주로 bias은 건들지 않는게 좋은 방법이라고 알려져있다. regularization도 할 필요가 없다. 오히려 weight에 집중하는 것이 성능 향상과 이어진다.)
6) Batch Normalization: Neural networks 학습단계에서 activation 값이 normal distribution을 갖도록 강제하는 기법으로, (내부의 activation shift에 의한 saturation을 방지할 뿐만 아니라, 몇 neuron이 과도하게 학습되는 것을 방지한다. 또한, normal distribution을 갖게만들어 regularization 효과와 큰 learning rate를 가질 수 있어 학습을 빠르게 진행할 수 있다는 것이 장점이다. 자세한 것은 batch normalization 논문을 읽어보는게 큰 도움이 된다.)
Regularization
(Neural networks를 학습할 때, neural networks의 parameter는 너무 많은데, data의 수는 너무 적은 경우가 많다. (거의 대부분이다.) 이 경우, networks의 capacity를 크게 갖으면서 (즉, 더 복잡한 feature를 배우도록 하면서) generalization capability를 상승시키기 위해서는 적절한 regularization 방법을 도입하는 것이 매우 중요하다.)
1) L2 regularization: 모든 parameter의 square만큼의 크기를 objective function에 더함으로써, weight의 크기에 제한을 두는 방법이다. 또한, weight에 제한을 둚으로써, weight 값을 가능한 널리 퍼지도록 하는 효과를 준다. 즉, 몇몇 input data에만 강하게 weight을 갖게하지 않으면서, 모든 input data에 모든 weight이 약하게 적용되게 함으로써, 좀 더 다양한 feature를 배우도록 한다. Gradient descent 과정에서, weight decay에 의해서 weight이 선형적으로 감소한다.
2) L1 regularization: 모든 parameter의 square값이 아닌 absolute 값을 objective function에 더함으로써, weights의 크기에 제한을 두는 방법이다. L1 regularization은 weight vector를 sparse하게, (0에 가깝게) 만드는 특징을 갖고 있어, feature selection에 사용될 수 있으며, input data의 sparse한 부분만 사용함으로 noisy input data에 거의 영향을 받지 않는다. L2 regularization을 적용하면 최종 weight vector는 작은 값들이 퍼져있는 형태이다. 만약 feature selection 후에 학습하는 것이 아니라면 많은 경우에 L2 regularization을 사용하면 좋은 성능을 기대할 수 있다. (모든 weight들이 어느 특정 값을 갖고 있고, 그 값이 서로 다른 시작점 (e.g., random initialization)을 갖고 있었다면, 서로 다른 feature를 배웠을 것이라는 기대가 있는 것이다.)
3) Max norm constrain: regularization 기법 중 하나로, weight vector의 길이가 미리 정해 놓은 bound 값을 넘지 못하도록 제한하면서 gradient descent 연산도 제한된 조건 안에서만 계산하도록 하는 projected gradient descent를 사용함. (이런 방법들은 아예 값을 제한함으로써, regularization을 가하는 방법인데, 큰 learning rate를 갖더라도 explode하지 않는 장점을 갖고 있다. 이와 연관된 technique이 clip gradient로 볼 수 있다. 하지만, 어느 값을 bound로 설정할 지에 대한 tuning이 필요하다.)
4) Dropout: 효과적인 regularization 방법으로 다른 regularization (L1, L2, maxnorm)과 상호 보완적인 방법이다. (핵심은, 각 neuron의 출력을 끄고 키는 과정을 통해서, 단일 structure에 다양한 network의 structure를 생성해낸 이후, 이 structure를 ensemble 하는 형태로 결정을 내린다는 것이다.)
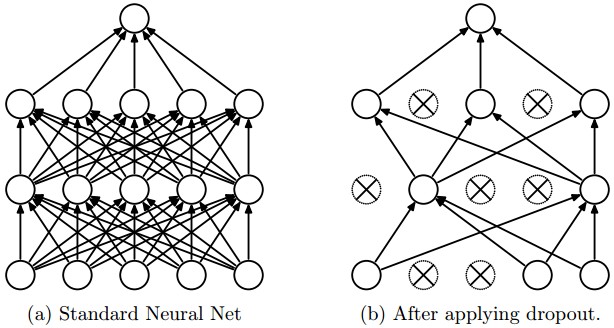
Dropout은 forward pass에 stochastic 접근을 도입하는 것이다. (noise를 넣는 형태) 동일한 관점에서 DropConnect는 forward pass 동안 weight을 0으로 만드는 것이다. (neuron을 아예 꺼버리는 게 아닌) 이 경우, 다양한 조합이 가능하여 Dropout보다 더 좋은 regularization을 유도할 수 있다.
Loss function
특정 구현된 network은 objective function (or loss function)을 최소화하는 것을 목표로 한다. (즉, 실제 label과 network가 예측한 label 사이의 차이를 보고 loss를 계산하고, 이 loss를 줄이는 것을 목표로 하는 것이다.)
1) Classification: SVM에서 볼 수 있는 loss function은 Weston Watkins formulation 이다.
두번째 다른 선택은 cross entropy를 사용하는 softmax classifier이다.
Class의 개수가 많은 경우에, Hierarchical Softmax를 사용하는 것이 도움이 된다.
2) Attribute classification (Skip)
3) Regression
(L2 norm을 사용하는 경우는 cross entropy를 사용하는 case보다 더 gradient가 작은데, 이는 http://neuralnetworksanddeeplearning.com/의 "Improving the way neural networks learn"을 참고하길 바란다. 따라서, regression 문제를 classification으로 바꿀 수 있으면 바꾸는 것이 최종 성능에 유리하다.)
'Deep learning study > CS231n' 카테고리의 다른 글
| Transfer Learning and Fine-tuning Convolutional Neural Networks (0) | 2019.03.02 |
|---|---|
| Understanding and Visualizing Convolutional Neural Networks (0) | 2019.03.02 |
| Convolutional Neural Networks: Architectures, Convolution / Pooling Layers (0) | 2019.03.02 |
| Neural Networks Part 3: Learning and Evaluation (0) | 2019.03.02 |
| Neural Networks Part 1: Setting up the Architecture (0) | 2019.03.01 |


