| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 시계열 분석
- Interpretability
- 메타러닝
- Explainable AI
- Deep learning
- Cam
- grad-cam
- python
- Machine Learning
- keras
- 백준
- SmoothGrad
- AI
- meta-learning
- Score-CAM
- 기계학습
- 코딩테스트
- Class activation map
- 인공지능
- 설명가능한
- Artificial Intelligence
- xai
- 설명가능한 인공지능
- 코딩 테스트
- Unsupervised learning
- coding test
- GAN
- cs231n
- 딥러닝
- 머신러닝
- Today
- Total
iMTE
Neural Networks Part 1: Setting up the Architecture 본문
Neural Networks Part 1: Setting up the Architecture
Wonju Seo 2019. 3. 1. 21:35Reference:
http://cs231n.github.io/neural-networks-1/
http://aikorea.org/cs231n/neural-networks-1/
Introduction
- Neural networks는 단순히 행렬 (matrix)와 벡터 (column vector)간의 연산으로 나타낼 수 있다. 예를 들어, W가 [10 x 3072], x가 [3072 x 1]의 크기를 갖고 있다면, (CIFAR-10 경우) 최종 출력 score (class와 연관된 점수)는 다음과 같이 표현될 수 있다.
-
- Neural network는 행렬 연산에 특정 non linear function을 적용하는 형태로 구성된다. 예를 들어, 다음과 같이 max 함수를 사용하는 단계를 추가하면, 2층 layer로 구성된다.
-
- 이때, W1는 [100 x 3072], W2는 [10 x 100]으로 정의된다. 그리고 max함수는 non linear function으로 각 원소에 적용된다. (element-wise) 만약, non linear function이 없는 경우 아무리 깊게 쌓더라도 하나의 weight으로 표현되므로 의미가 없다. W2와 W1의 parameter는 stochastic gradient descent로 학습이되며, gradient는 backpropagation으로 계산된다.
Modeling one neuron
Neural network 영역은 원래 생물학적 신경계 모델링의 목표로 고무되었지만, 이후 기계 학습 과제에서 엔지니어링 문제가 되어 좋은 결과를 얻었다. (지금의 많은 technique들은 신경계에서 모델링을 했다기 보다는, 수학적, 통계적 기술들을 기반으로 한다.)
기본적으로 하나의 neuron을 단순힌 weighted sum으로 modeling할 수 있다. 즉, input vector x에 weights을 곱하고 (수상 돌기가 입력 신호를 받아들임.) 이 값을 특정 activation을 통과시키고 이 activation이 특정 threshold (임계값)를 넘어가는 경우 신호를 전달한다. (축색삭 돌기를 따라 출력 신호가 전달됨.)
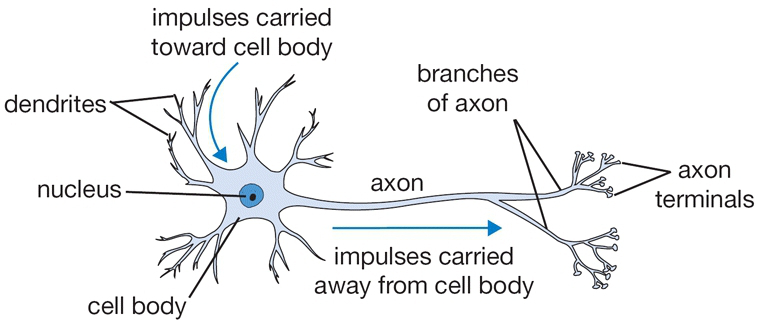
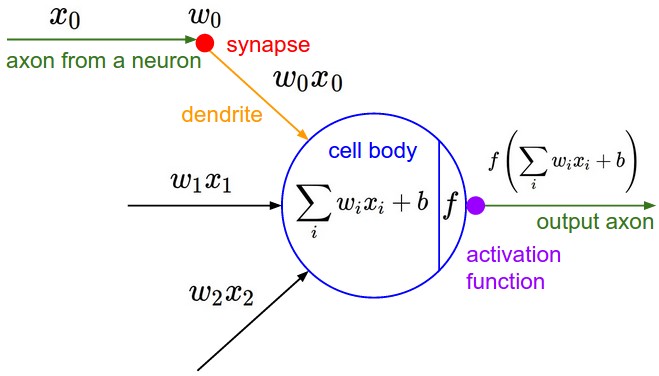
역사적으로, activation function의 선택은 sigmoid를 사용하는데, 이 sigmoid function은 weighted sum을 입력으로 받아들이고 0과 1 사이의 범위로 축소하기 때문이다. (0과 1 사이는 확률이 나타낼 수 있는 치역에 해당한다.) 즉, 각 뉴런은 입력과 그 가중치로 내적을 수행하고, bias를 더한 다음에 non-linear function (예, sigmoid function)을 적용함.
Single neuron as a linear classifier
선형 분류기에서 보았듯이, neuron은 input space에서 특정 선형 영역을 선호하거나 (거의 활성화), 싫어하는 (0에 가까운 활성화) 능력을 갖는다. neuron의 출력에 적절한 loss function을 추가함으로, 단일 neuron을 linear classifier로 바꿀 수 있다.
1. Binary softmax classifier
위의 식은 weighted sum에 sigmoid function을 취한 형태이고, 이는 다음과 같은 확률 개념으로 이해할 수 있다.
그렇다면, 다른 class (즉, 0)에 대한 확률은 다음과 같이 계산된다.
(확률의 합은 무조건 1이다.)
Linear classification section에서 본 것 처럼 cross entropy loss를 공식화 할 수 있으며, 이를 최적화 하면 binary softmax classifier가 된다. (logistic regression) Sigmoid function이 0~1로 제한되므로, 특정 class의 확률이 (출력)이 0.5보다 크면 그 class로 분류한다.
2. Binary SVM classifier
max-margin hinge loss를 neuron의 출력에 연결하고 학습하여 binary SVM이 되도록 학습시킬 수 있다.
3. Regularization interpreation
SVM과 softmax 경우에 regularization loss는 'gradual forgetting'으로 이해할 수 있는데, 이는 모든 weights이 update이후에 0을 향하도록 하기 때문이다.
Commonly used activation functions
모든 activation function은 (or non-linear function) 단일 숫자를 취하여 고정된 수학 연ㅅ나을 수행한다.
1. Sigmoid
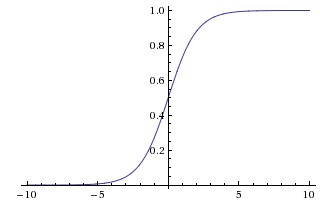
Sigmoid function은 다음과 같이 표현된다.
특정 실수 값을 취하고, 0과 1 사이 범위로 줄여주는 역할을 한다. 큰 음수는 0이되고 큰 양수는 1이되는 saturation 성질을 갖고 있다. 하지만, saturation이 되는 구간에서는 gradient가 0가 되어, chain rule로 gradient가 곱해질 때, gradient가 0이 되는 효과가 나타난다. 초기 weight이 크다면 neuron이 saturation되어 network의 학습이 어렵다.
Sigmoid 출력이 zero-centered가 아니고, 항상 양의 값이다. layer의 neuron이 zero-centered가 아닌 입력을 받음으로 바람직하지 않다. (개인적으로 생각할 때, layer사이의 출력이 zero-centered가 아닌 경우, 특정 bias가 있는 것이라고 볼 수 있고, 이 bias로 인해서 항상 어느 값 이상이 나옴으로 saturation되는 등의 문제가 발생하는게 아닐까하다. 혹은, zero-centered된 데이터는 학습에 아주 적절한데, layer를 통과하면서 zero-centered가 아니게 되면서, 다음 layer가 학습하기가 어려운 형태가 됨으로 학습이 느려지는 것일 수도 있다.)
이 문제는 saturation문제에 비해 덜 심각하다.
2. Tanh (Hyperbolic Tangent)
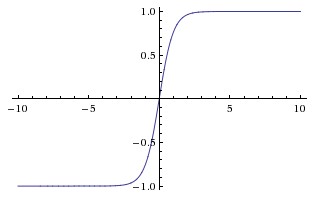
tanh 는 sigmoid function과 비슷한 S형태의 함수인데, 범위가 [0,1]가 아닌 [-1,1]이다. Sigmoid function과 마찬가지로 saturation되는 문제가 있으나, zero-centered인 특징을 갖고 있다.
(S자형 함수들은 항상 saturation되는 문제를 갖고 있으므로 gradient vanishing problem에 취약하다. 이를 해결하는 방법이 최대한 gradient를 크게 유지하는 함수를 activation function을 찾는 것이고, ReLU가 이에 해당한다. 부분 선형을 통해서 gradient를 크게 유지함으로 gradient vanishing problem을 해결한다.)
3. ReLU (Rectified Linear Unit)
f(x)=max(0,x)로 나타내며 몇가지 장단점을 갖고 있다.
1) sigmoid/tanh에 비해서 saturation이 되지 않으므로 stochastic gradient descent에서 수렴이 빠르다.
2) tanh/sigmoid에 비교해서 ReLU는 연산이 매우 단순하다.
3) ReLU는 훈련 중에 죽을 수 있다. (dead ReLU) activation이 0미만이 됨으로 neuron이 죽어서 학습이 되지 않는다. (gradient가 0이되어 backpropagation으로 전파되는 요소가 0이된다.)
4. Leaky ReLU
Dead ReLU를 해결하기 위해서 x<0 일때, 0이 되는 대신에 작은 음의 기울기를 가진다. 그 기울기 값을 정해줘야하는 case (Leaky ReLU)가 있고, 학습을 통해 학습할 수 있는 case인 Parameteric ReLU (PReLU)가 있다. (보통 ReLU 대신에 ReLU variant들을 사용하는 것이 학습에 유리하다는 보고가 있다.)
5. Maxout
위의 형태로 표현되며, ReLU와 leaky ReLU의 general한 version의 activation function이다. neuron이 죽는 등의 문제를 겪지 않으면서 ReLU의 장점을 얻을 수 있지만, parameter가 2배가 된다는 것이 단점이다. (w1,b1,w2,b2를 학습해야한다.)
Neural Network Architecture
Layer-wise organization
Neural network는 비순환 graph로 연결된 neuron collection으로 모델링 된다. 일반적인 neural network의 구조는 fully-connected layers이며, 인접한 두 layer간의 neurons이 완전히 연결되어 있는 형태를 나타내며, 같은 layer내의 neuron의 연결은 없다.
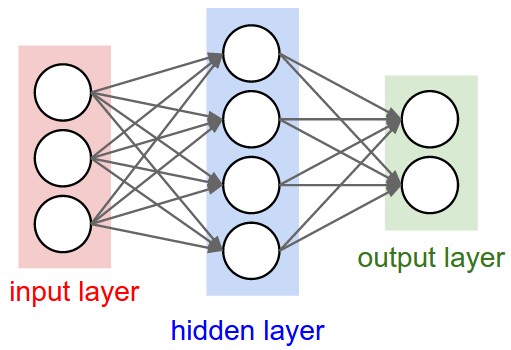
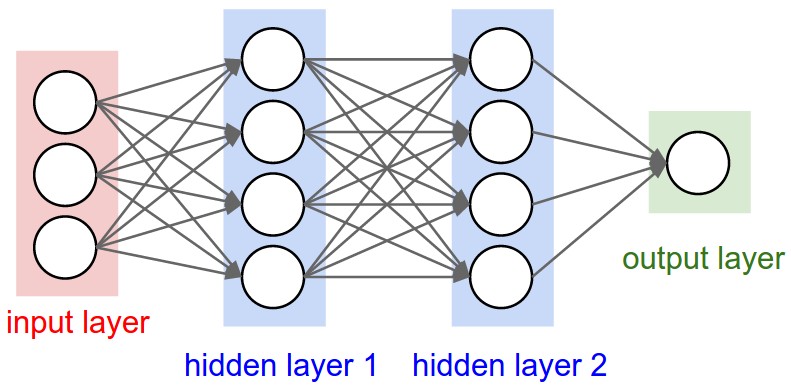
Single layer는 hidden layer가 없는 network로 logistic regression 혹은 SVM이 single layer의 특별한 경우이다. 출력 layer의 activation이 linear인 경우 regression problem, softmax 혹은 sigmoid인 경우 class score를 출력하므로 classification problem이 된다.
Example feed-forward computation
Feed-forward 연산은 단순히 행렬 곱셈 - activation function 적용 - 행렬 곱셈... 등으로 연산이 반복되고 출력 layer에서 특정 class의 score 혹은 value를 계산한다.
Representational power
Fully-connected neural networks는 network의 weights로 parameterized된 function이다. 이런 함수가 나타낼 수 있는 representation power가 무엇인지에 대한 질문이 나올 수 있다.
적어도 hidden layer가 있는 neural network는 "Universal approximators"이고, 신경망은 모든 연속 함수를 근사할 수 있다. 그렇다면 하나의 hidden layer로 모든 함수를 구할 수 있다면 왜 굳이 더 많은 layer를 사용하여 deep한 network를 구성해야하는 건가?
(여기서 설명하는 내용은 다소 직관적인것 같지 않아서, 내 개인적인 이해를 적고자한다. Neural network는 계층적인 구조로 low level의 feature를 구현한 후, 이 feature들이 조합하여 high level feature가 구현됨으로써, Representation power가 강력해진다. 따라서 여러 층을 깊게 쌓는 것이 한층을 넓게 하는 것보다 장점을 갖고 있으며, parameter의 개수에서도 이점을 갖는다.)
Setting number of layers and their sizes
Neural network에서 layer의 크기와 깊이를 증가시키면 network의 capacity가 증가한다. neuron이 많은 다른 기능을 표현하기 위해 협력할 수 있기 때문에 표현할 수 있는 function의 공간이 커진다. 더 큰 neural network는 더 복잡한 기능을 나타낼 수 있다.
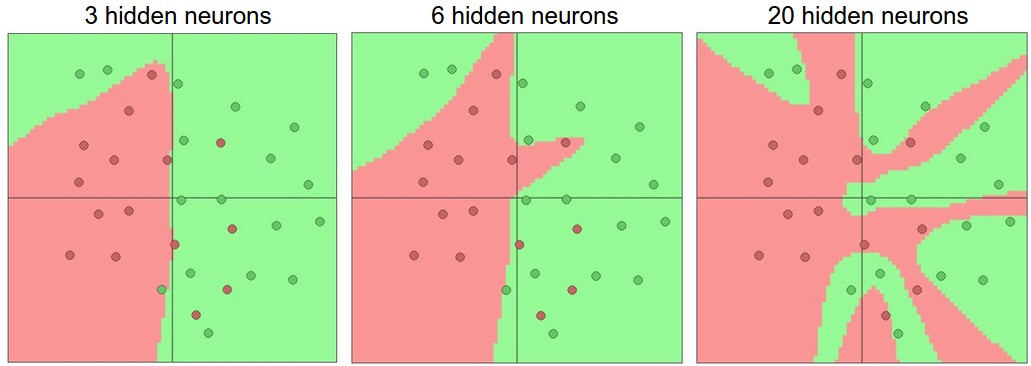
더 많은 neuron을 가진 neural networks가 더 복잡한 기능을 표현할 수 있는데, over-fitting이 발생하여 데이터의 잡음을 학습하게된다.
데이터가 간단하다면 작은 neural network를 선호할 수 있으나, "이는 잘못된 것이다." 우리는 최대한 neural network가 충분히 복잡한 기능을 학습할 수 있는 capacity를 갖도록 구현하고, over-fitting을 방지하는 (L2 regularization, dropout, input noise)등의 방법을 사용함으로써 neuron의 수보다는 over-fitting을 제어하는 것이 더 좋은 방법이다.
"더 작은 network가 gradient descent와 같은 local 방법으로 훈련하기가 더 어렵다는 것이다." loss function의 local minima가 비교적 적지만 minma의 많은 부분이 수렴하기 쉽고 loss가 나쁘다. 반대로, 더 큰 neural network는 훨씬 더 많은 local minima를 포함하지만, 이 최소값은 실제 loss의 측면에서 더 유리하다. (작다는 의미) + 행운에 덜 의존한다. (작은 network의 작은 loss는 운에 좌우되는 경향이 있는 것으로 보인다. 하지만 큰 network는 운에 덜 의존하면서 loss가 상당히 비슷하면서 낮은 경향이 있다.)
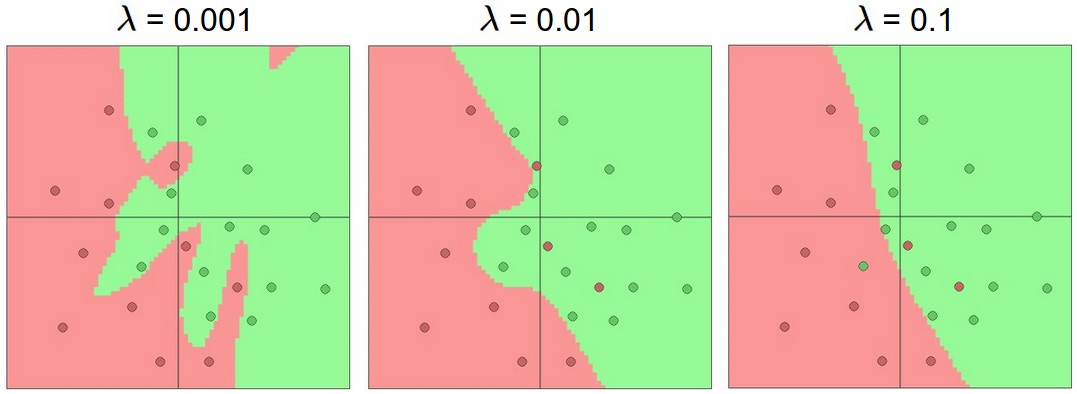
Regularization의 강도는 neural network의 over-fitting을 해결하는데 선호된다. 다음은 regularization강도에 따른 모델의 decision boundary의 형태를 나타내고 있다.
'Deep learning study > CS231n' 카테고리의 다른 글
| Transfer Learning and Fine-tuning Convolutional Neural Networks (0) | 2019.03.02 |
|---|---|
| Understanding and Visualizing Convolutional Neural Networks (0) | 2019.03.02 |
| Convolutional Neural Networks: Architectures, Convolution / Pooling Layers (0) | 2019.03.02 |
| Neural Networks Part 3: Learning and Evaluation (0) | 2019.03.02 |
| Neural Networks Part 2: Setting up the Data and the Loss (0) | 2019.03.02 |


