| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 설명가능한
- SmoothGrad
- Deep learning
- 메타러닝
- Artificial Intelligence
- python
- 백준
- Cam
- coding test
- meta-learning
- cs231n
- grad-cam
- 코딩테스트
- 딥러닝
- 시계열 분석
- keras
- 설명가능한 인공지능
- 기계학습
- Explainable AI
- GAN
- Score-CAM
- Unsupervised learning
- Class activation map
- 머신러닝
- xai
- AI
- Machine Learning
- 인공지능
- Interpretability
- 코딩 테스트
- Today
- Total
iMTE
Neural Networks Part 3: Learning and Evaluation 본문
Neural Networks Part 3: Learning and Evaluation
Wonju Seo 2019. 3. 2. 13:21Reference:
http://cs231n.github.io/neural-networks-3/
http://aikorea.org/cs231n/neural-networks-2-kr/
(이번 section 내용은 100 % 번역이 위의 주소에 잘 되어 있다.)
Learning
이전 sections에서는 layer를 쌓고, layer의 units을 준비할지 (network connectivity), 데이터를 어떻게 준비하고, 어떤 손실 함수 (loss function)을 선택할지에 대해서 다루었다. 본 section에서는 parameter를 학습하고 좋은 hyper-parameter를 찾는 과정에서 다룰 예정이다.
Gradient checks
Numerical 방법으로 계산한 gradient과 Analytic 방법으로 계산한 gradient를 비교하는 것을 Gradient check라고 한다.
같은 근사라 하여도 이론적으로 더 정확도가 높은 근사 공식이 있다. Gradient를 Numerical 근사한다면, 다음 식을 떠올릴 수 있다.
h는 매우 작은 수가 사용되며, 위 식보다는 아래의 centered differential formulation이 경험적으로 훨씬 낫다.
이 공식은, 맨 위의 식보다 계산량이 두배 많지만, 훨씬 더 정확한 근사를 제공한다. 첫 식은 O(h)의 오차가 있는데 반해, 두번째 식은 오차가 O(h^2)이다. (by Taylor Expansion) (h가 작은 수인데, 이 작은수를 제곱하였으므로 오차가 매우 작아진다. 즉, 근사가 정확해진다.)
Use relative error for the comparison: Analytic gradient 참값과 numerical gradient 근사 값과 비교하기 위해서는 절대 오차를 추적하여 어느 한계점 (threshold)를 넘으면 gradient error라고 할 수 있다. (하지만, absolute오차에는 문제가 있는데, 기준에서 문제가 있다. 그 threshold를 어떻게 설정하는 지에 대한 의문) 대신에, 절대 오차와 두 gradient의 비율을 고려하는 relative error가 더 적절하다.
1) 상대오차 > 1e-2, gradient 계산이 잘못 되었다.
2) 1e-2>상대오차>1e-4, 불편함을 느끼자.
3) 1e-4>상대오차, 꺾임이 있는 (미분이 불가능한 부분, ReLU가 그 예이다.) objective function에서는 괜찮지만, tanh 혹은 fotmax를 쓰는 objective function 처럼 꺾임이 없다면 1e-4는 너무 크다.
4) 1e-7 혹은 그 보다 작은 상대 오차라면, 행복을 느껴야 한다.
Error가 층을 올라가며 축적되므로 relative error는 layer의 개수가 많아질 수록 (deeper network)에서 커진다.
(Gradient check에 대한 팁들이 제공되고 있는데, 이 부분은 aikorea.org/cs231n/neural-networks-3/에서 잘 설명하고 있고, 이정도의 내용은 직접 network를 코드로 구성하는 경우가 아니면 참고하지 않아도 된다고 생각하기 때문에 skip 한다.)
Before learning : sanity checks tips/tricks
1. Loo for correct loss at chance performance : 적은 수의 parameter로 초기화 할 때, 기대한 loss 값을 얻는지 확인해야한다.
2. Regularization strength를 올릴 수록 loss function의 값이 올라가야 한다.
3. Overfit a tiny subset of data : 전체 데이터 셋으로 훈련을 시작하기 전에, 작은 부분으로 훈련을 시도해보고, 0이 cost를 달성하는지 확인하여 보라. 작은 자료에서 이러한 확인 과정이 제대로 끝나지 않으면 전체 데이터셋으로 확장하는 것은 무가치하다. (하지만, 이는 작은 훈련 데이터가 적합이 되었다고 하더라도 전체 데이터가 그럴 것이라고 하는 것은 무리가 있다.)
Babysitting the learning process
Neural networks를 훈련하는 과정에서 몇몇 quantity는 monitoring을 해야 한다. 이런 quantity는 training의 process를 지켜볼 수 있도록 하며, 효율적인 학습을 위한 hyper-parameter 조정에 대한 직관을 얻을 수 있다.
Plot의 x축은 항상 epoch을 단위로 한다. Epoch은 전체 training samples이 몇번이나 training에 사용되었는가 재는 용어다. Iteration number는 batch size의 선택에 따라 임의로 바뀔 수 있다.
Loss function
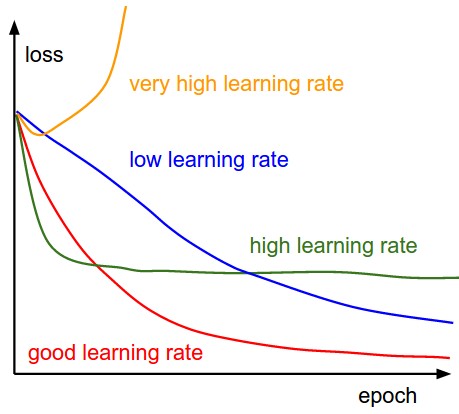
Training 과정에서 매 epoch마다 loss를 계산한 결과를 plot한다. 훈련 과정에서 learning rate의 영향이 위의 그림에 잘 표현되어 있다. 낮은 learning rate는 선형적인 성능 향상으로 이어진다. 높은 learning rate는 좀 더 지수적 (exponential)한 향상으로 이어진다. 더 큰 learning rate는 loss의 감소를 가속하지만, 더 나쁜 loss를 초래할 수 있다. 그 이유는 parameter의 큰 변화로 이어지고 큰 loss를 초래한다. (보통, 작은 learning rate를 사용하는 경우 최종적으로 더 나은 performance로 이어질 수 있다. 하지만 시간이 많이 걸리기 때문에, 큰 learning rate를 유지하면서, loss를 낮추려고 하는 시도들이 진행되고 있다. Batch normalization가 그 중 하나가 된다.)
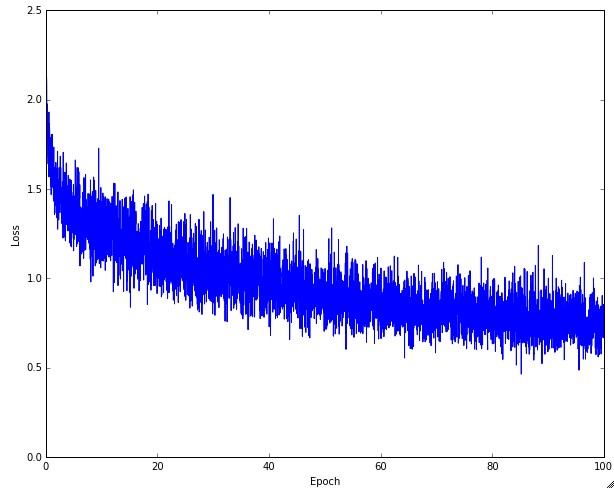
Loss function의 fluctuations은 batch size와 연관이 있다. 만약 batch size가 1이라면, 훨씬 더 많이 fluctuating 한다. 만일 batch size가 전체 데이터 셋의 크기와 같다면, fluctuation이 최소화 된다.
Train/Val Accuracy
Training/validation accuracy는 classifier의 훈련시 추적해야할 또 다른 중요한 값이다. 이 plot은 model이 over-fitting 중인지 발견할 수 있는 직관을 제공한다.
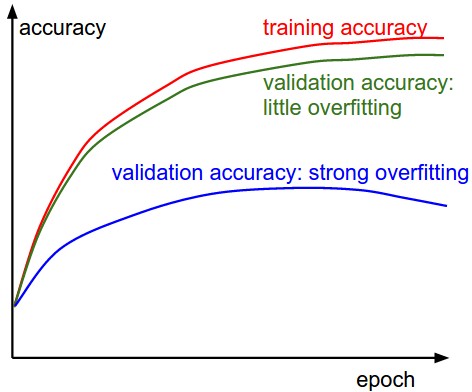
Validation error 곡선은 training error에 비해서 매우 높은데, 이는 over-fitting을 의미한다. 실제로 이러한 현상이 나타나면, regularization을 쓰거나 더 강한 L2 penalty나 dropout을 쓰거나, 혹은 데이터를 더 모으는 과정을 사용할 것이다. 다른 가능성으로는, validation error가 training error를 잘따라가는 것인데, 이는 model의 capacity가 충분히 높지 않은 문제가 있다. (우리는 이러한 현상을 Under-fitting이라고 한다.) 이 경우, parameter의 개수를 늘려서 model의 capacity를 증가시킨다.
Ratio of weights: updates
Weight의 현재 크기와 update로 인한 변화량의 크기를 비교해 볼 수 있다. Vanila SGD에서는 learning rate와 gradient의 곱이 바로 변화량이다. (이는, update식을 볼 수 있다.)
Activation/Gradient distributions per layer
올바르지 않은 weight initialization은 training process를 느리게 하거나 와전히 망칠 수 있다. activation과 gradient 값의 histogram을 network의 모든 layer마다 그려보는 것이다. 직관적으로, 만일 이상한 분포가 나온다면 나쁜 징조이다. 예를 들어, tanh neuron에서는 활성 값이 [-1,1]의 전 범위에 걸쳐 분산되어 있는 것이 좋은데, 모든 활성값이 0을 내놓거나 -1 혹은 1에 집중되어 있다면 (saturation) 문제가 있는 것이다.
First-layer visualization
마지막으로 feature를 시각화 하는 것이 많이 도움이 된다. Neural network의 first layer weight를 시각화 한 예, 좌측은 feature에 noise이 많을 때 나타날 수 있는 증상이다. (수렴하지 않은 network, 적절하지 않은 learning rate, 매우 낮은 regularization penalty) 우측은 부드럽고 깨끗한 다양한 feature 값이 보이는 경우로, 잘 학습된 경우라고 볼 수 있다.


Parameter updates
이전 part에서 gradient check 와 학습이 잘되는지를 확인하는 process를 다뤘다면, 이제는 backpropagation으로 계산된 gradient가 실제로 parameter에 어떻게 update를 하는지를 확인하고자 한다.
1. SGD and bells and whistles
1) Vanila update : 가장 간단한 update는 gradient의 반대방향으로 parameter를 update하는 것이다. (Gradient는 특정 function이 가장 크게 증가하는 방향을 가리키는데, 이 방향을 반대로 가면 그 특정 function이 감소한다는 직관을 얻을 수 있다.)
2) Momentum update : Deep networks에서는 Vanila update보다 더 잘 수렴한다. 이 방법은 optimization problem을 물리학적 관점에서 바라보는 데서 유래했다. (더 나은 설명은, 이전 gradient의 변화를 반영하여 현재 gradient를 변화시킴으로써, 이전의 특정 방향을 유지하는 것이 momentum 방법이다. 이 방법은 zigzag로 인해 training이 불안전해지는 현상을 방지한다.)
3) Nesterove momentum : 원래 x 위치였다면, 그 위치의 gradient를 반영하여 미래 위치로 이동하고 그 위치에서 gradient를 계산하는 방법이다. 이 방법은 좀 더 빠르게 수렴할 수 있는 장점을 지닌다.
Annealing the learning rate
Deep neural networks에서 시간에 따라 learning rate를 조정하는 것은 언제나 도움이 된다. 천천히 learning rate를 감소시키거나, 어느 특정 epoch에서 감소시키는 방법이 사용된다.
1) Step decay : 몇 epoch마다 일정량만큼 learning rate를 줄인다. 실전에서는, 우선 고정된 learning rate로 validation error를 살펴보다가, validation error가 개선되지 않을 때마다 learning rate를 감소시키는 방법을 택하기도 한다.
2) Exponential decay : 다음 식이 learning rate 변화를 설명하고 있다.
a_0와 k는 hyper-parameter이고, t는 반복 횟수이다.
3) 1/t 감소 : 다음 식이 learning rate 변화를 설명하고 있다.
a_0, k는 hyper-parameter이고 t는 반복 횟수이다.
실전에서는 step decay가 좀 더 선호되는데, hyper-parameter 설정이 k에 비해서 해석이 더 쉽기 때문이다.
Second order methods
Newton's method를 사용해서 1차 미분 접근이 아닌 2차 미분 접근으로 optimization problem을 해결할 수 있다.
Hf(x)는 Hessian matrix로, 2차 미분으로 이루어진 square matrix이다. 직관적으로 Hessian matrix는 어떤 함수의 curvature를 뜻하고, 이 정보를 사용해서 더 효율적인 update를 수행할 수 있다. (기울기의 변화율을 아는 것은 loss function의 형태에 대해서 어느정도 이해가 있다고 볼 수 있다. 따라서, 1차 미분 접근에 비해서 더 효율적인 update가 가능하다.)
특별히, Hessian matrix의 inverse matrix를 곱함으로써, 휨이 약한 방향으로는 더 크게, 휨이 강한 방향으로는 짧게 움직일 수 있다. 1차 근사 방법에 비해서 Newton's method의 강점은 learning rate에 대한 hyper-parameter가 없다는 것이다.
하지만, 위 방법은 Hessian matrix를 계산해야하고, 이 matrix의 inverse를 계산해야하므로 많은 시간과 메모리가 필요하다. 그 결과 유사 뉴턴 method이 inverse hessian matrix를 근사하기 위해 고안되었다. 이들 중, L-BFGS가 가장 대중적이다.
실제 응용에서는 L-BFGS나 다른 2차 근사 방법이 대규모 deep learning에서 사용되지 않는 것이 보통이다. 표준적으로는 SGD와 its variants이 훨씬 간단하고 계산이 빨라서 많이 사용된다.
Per-parameter adaptive learning rates
지금까지 방법은 모든 parameter에 동일한 learning rate를 적용하였다. Parameter별로 learning rate를 다르게 하고 이를 data adaptive하게 접근하려는 노력이 있었다. 이러한 방법들은 보통 또다른 hyper-parameter를 필요로 하지만, 이 hyper-parameter는 넓은 범위에서 잘 작동하여 일반 learning rate tuning보다는 덜 까다롭다. (어느 weight에는 1e-5가 다른 weight에는 1e-3등이 최적화에 필요하다면, 서로 다른 weight을 적절하게 update하기 위한 방법이 제안될 수 있다.)
1) AdaGrad : 높은 gradient를 갖는 weight들은 learning rate가 감소하고, gradient 값이 낮거나 업데이트가 거의 없는 weight들은 learning rate가 증가한다. 하지만, 쉽게 learning rate이 작은 값을 갖게 되어 학습이 너무 빨리 멈출 수 있다.
2) RMSProp : Adagrad와 같은 방법이나, learning rate를 감소시키는 것을 moving average를 사용하여서 과거의 gradient에 대한 memory를 지우면서 update를 한다. 이 방법을 사용해서 학습이 너무 빨리 멈추는 것을 방지한다.
3) Adam : RMSProp에 Momentum을 혼합한 형태이다.
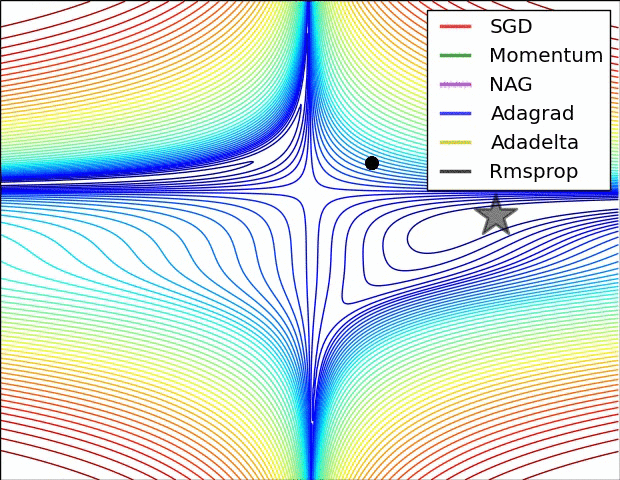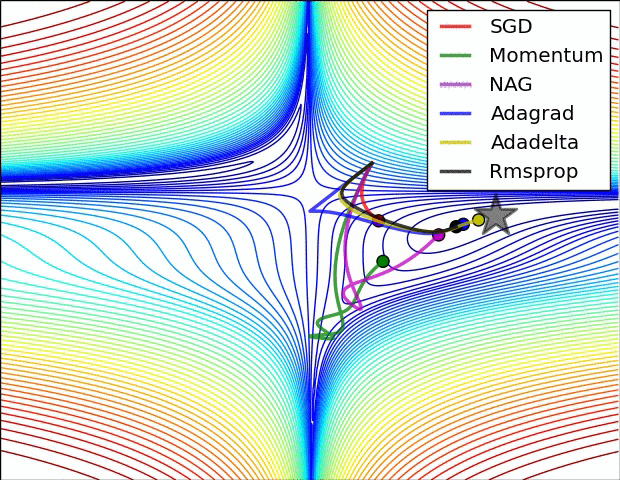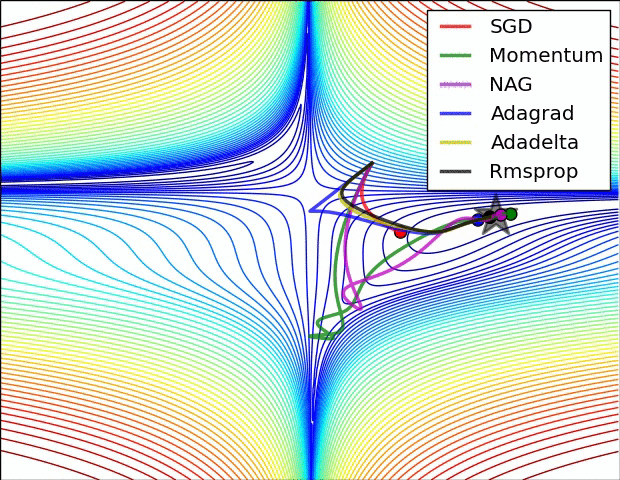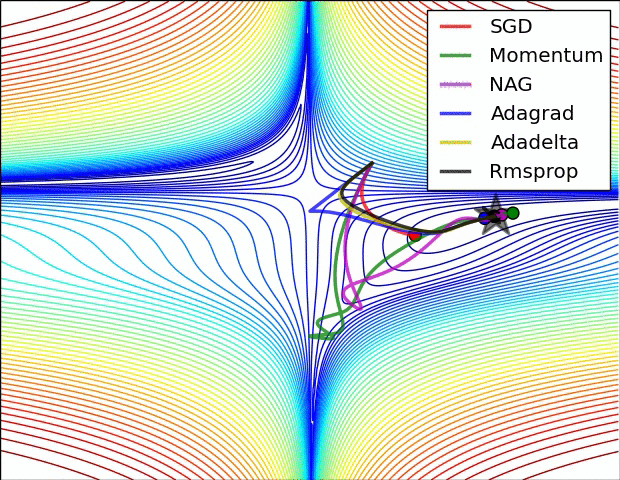
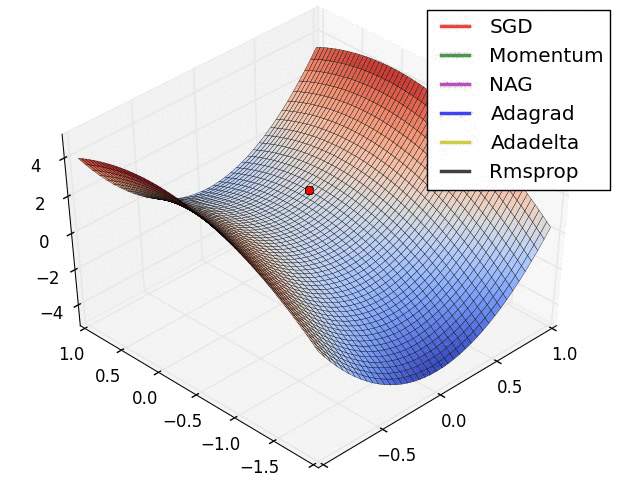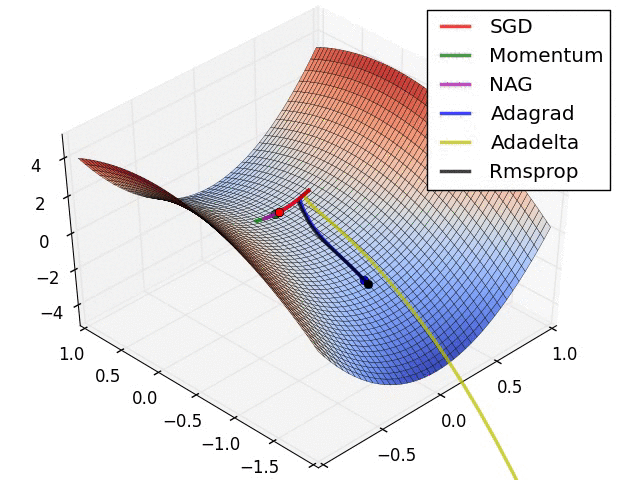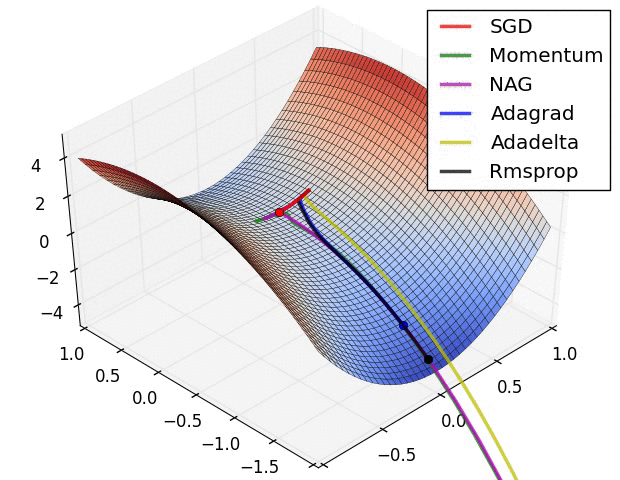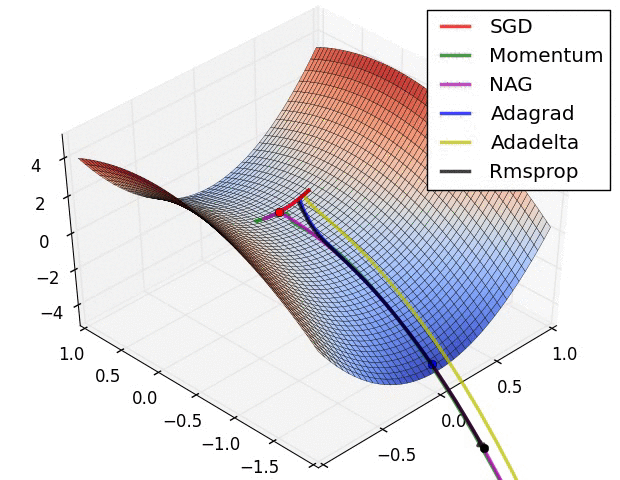
Hyper-parameter optimization
Deep neural networks에는 많은 hyper-parameter가 관련된다. 예를 들어, learning rate, learning rate decay schedule, regularization strength 등이 있다.
1) Implementation : hyper-parameter를 임의로 선택하여 optimization을 수행하는 worker를 만들자. checkpoints를 저장하게 만듦으로써, hyper-parameter tuning을 한다.
2) Prefer one validation fold to cross-validation : 많은 경우에, 적당한 크기의 validation set을 설정해 두어 한 번만 검증하는 것이, 여러 번의 교차검증보다 코드를 더 단순화한다.
3) Hyper-parameter ranges : log scale에서 hyper-parameter를 찾는 것이 중요하다. 직관적으로 learning rate와 regularization strength는 multiplicative 효과가 있다. Dropout rate는 보통의 scale에서 검색된다.
4) Prefer random search to grid search :
(Random search 방법이 grid search보다 optimum point를 잘 찾을 수 있다는 것이다. 하지만 먼저 Grid search를 진행하고 그 영역을 정해놓은 다음에 random search를 사용하는 것이 일반적인 방법이다.)
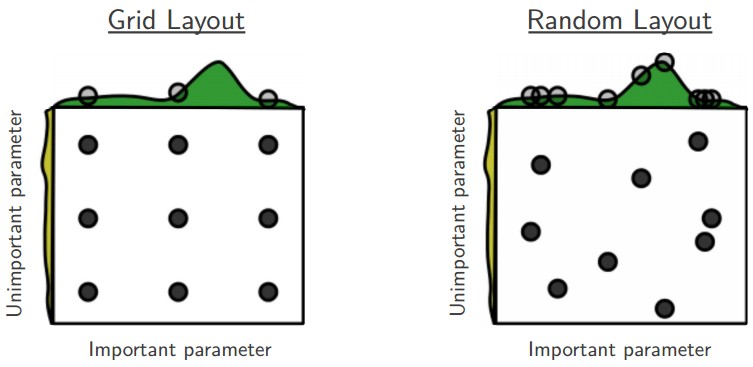
5) Careful with best values on border : 가끔은 hyper-parameter가 나쁘게 설정되었을 수도 있다. 최종 learning rate가 border에 있지 않아야한다. 그렇지 않으면, 더 최적의 hyper-parameter를 놓치고 있는 것일 수도 있다.
6) Stage your search from coarse to fine : 좁은 범위로 계속 range를 줄여나가자.
7) Bayesian hyper-parameter optimization : hyper-parameter를 평가할 때, exploration-exploitation의 trade-off에서 적절한 균형을 찾는 것이다. (현재 많이 진행되고 있는 연구 분야이다.)
Model ensemble
실제 neural network에서 성능을 향상시킬 수 있는 방법은 1) 여러 개의 독립적인 모형을 만들고 테스트 때 그들이 평균 예측을 취하는 것이다. 2) ensemble에 관여하는 model이 많아지면, 보통 성능은 단조적으로 개선된다. 게다가 ensemble 내에서 모형의 다양함이 늘어날 수록 성능의 개선은 더 극적이다.
Ensemble 구축방법.
1) same model, different initialization : 교차 검증으로 최고의 hyper-parameter를 결정한 다음, 같은 hyper-parameter를 사용하되, 초기값을 임의로 다양하게 여러 모형을 훈련. 위험성은, 모형의 다양성이 오직 다양한 초기값에서만 온다.
2) Top models discovered during cross-validation : 교차 검증으로 hyper-parameter를 결정한 다음에, 몇개의 최고 모형들을 선정하여 이들로 ensemble을 구축함. 이 방법은 ensemble 내의 다양성을 증대시키나, 준-최적 모형을 포함할 수 있는 위험이 있다.
3) Different checkpoints of a single model : 단일한 network의 checkpoint를 ensemble하여 제한적인 성공을 거둔 바 있다. 이 방법은 다양성이 떨어지지만, 실전에서는 합리적으로 잘 작동할 수 있다. (이 방법은 매우 간편하고 저렴하다는 점이 장점이다.)
4) Running average of parameters during training : 훈련 동안 (시간에 따른) weights 값의 exponentially decaying sum을 저장하는 제 2의 네트워크를 만들면 언제나 몇 퍼센트의 이득을 값싸게 취할 수 있다. (weight을 exponentially decaying sum으로 저장하면서 네트워크를 구현하면, minima에서 oscillating하고 있는 weight의 평균을 구할 수 있으므로 낮은 minima에 도달 할 수 있는 장점이 있다.)
5) 단점은 test sample에 모형을 적용할 때 평가에 더 많은 시간이 걸린다는 것이다.
'Deep learning study > CS231n' 카테고리의 다른 글
| Transfer Learning and Fine-tuning Convolutional Neural Networks (0) | 2019.03.02 |
|---|---|
| Understanding and Visualizing Convolutional Neural Networks (0) | 2019.03.02 |
| Convolutional Neural Networks: Architectures, Convolution / Pooling Layers (0) | 2019.03.02 |
| Neural Networks Part 2: Setting up the Data and the Loss (0) | 2019.03.02 |
| Neural Networks Part 1: Setting up the Architecture (0) | 2019.03.01 |



