| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- SmoothGrad
- cs231n
- Explainable AI
- python
- 백준
- Artificial Intelligence
- keras
- GAN
- 코딩 테스트
- 메타러닝
- 인공지능
- Score-CAM
- 설명가능한 인공지능
- Deep learning
- Interpretability
- 머신러닝
- 딥러닝
- xai
- 설명가능한
- AI
- grad-cam
- 코딩테스트
- Unsupervised learning
- meta-learning
- coding test
- Machine Learning
- Class activation map
- Cam
- 시계열 분석
- 기계학습
- Today
- Total
iMTE
Convolutional Neural Networks: Architectures, Convolution / Pooling Layers 본문
Convolutional Neural Networks: Architectures, Convolution / Pooling Layers
Wonju Seo 2019. 3. 2. 16:42Reference:
http://cs231n.github.io/convolutional-networks/
http://aikorea.org/cs231n/convolutional-networks/
ConvNet
ConvNet은 앞에서 다룬 일반 neural networks (feed forward라는 점에서 비슷하다.)과 유사하다. Weight과 bias로 구성되며, 각 neuron은 input을 받아 dot product를 한 뒤에 non-linear 연산을 진행한다. ConvNet은 마지막 레이어에 loss function을 갖고 있으며, 일반 neural networks 학습시킬 때 사용하던 각 종 기법을 동일하게 적용할 수 있다.
Architecture overview
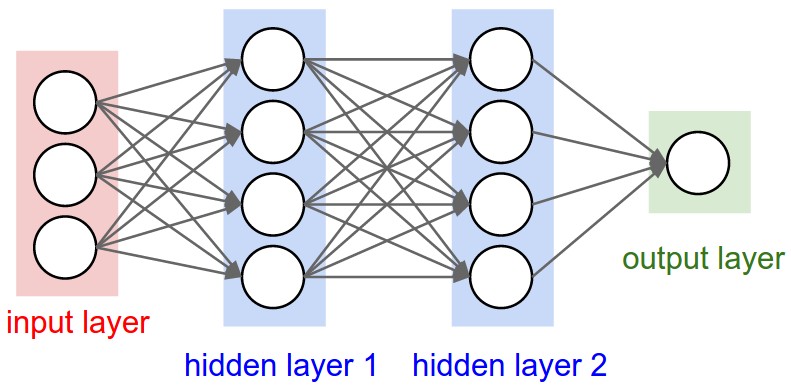
Neural networks는 vector를 일련의 hidden layer를 통해 transformation한다. 각 hidden layer는 neurons로 이루어져 있으며, 모두 연결되어 있는 구조를 갖는다. (fully-connected neural networks) 마지막 layer는 output layer로, classification problem에서 class score를 나타낸다.
일반적인 fully connected neural networks는 이미지를 다루기 힘들다. (만약 이미지의 size가 256 x 256 x 3이고 neuron이 100개라면, 256 x 256 x 3 x 100 개의 weight이 필요하다. 어마어마한 수다.) 따라서, fully connected neural networks의 구조는 심한 낭비이고, 대부분 over-fitting으로 이어진다. (많은 parameter의 수는 over-fitting으로 이어진다.)
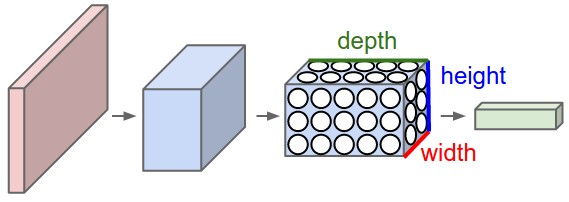
ConvNet은 input이 이미지로 이뤄져있는 특징을 좀 더 합리적으로 고려한 architecture를 갖고 있다. 일반적인 fully connected neural network와 달리 width, height, depth의 3차원 데이터를 분석한다. 밑의 왼쪽 그림은 fully connected neural network를, 오른쪽 그림은 ConvNet을 표현하고 있다.
Layers used to build ConvNets
ConvNet의 각 layer는 미분 가능한 transformation function을 통해 하나의 activation volume을 다른 activation volume으로 transform한다. 보통 ConvNet은 Convolutional layer, pooling layer, fully connected layer (요즘은 1x1 convolutional layer를 사용함으로 fully connected layer의 단점을 극복하고 있다.)라는 3종류의 layer가 사용된다.
1. Convolutional layer는 input image의 '일부 영역'과 연결되어 있으며, 이 연결된 영역과 weight과의 dot product를 계산하여 activation volume을 계산한다.
2. 각 element에 대해서 activation function을 적용한다.
3. Pooling layer는 width와 height에 대해 downsampling을 수행해서 volume의 width와 height를 줄인다.
4. Fully connected layer는 class score를 계산한다. 이전 volume의 모든 element와 연결되어 있다.
Convolutional layer와 fully connected layer는 parameter를 갖고 있지만, pooling layer와 ReLU function은 parameter를 갖지 않는다.
요약하면,
1) ConvNet architecture는 여러 layer를 통해 input image volume을 class score로 변환시킨다.
2) ConvNet은 Conv/FC/ReLU/Pool layer를 사용한다.
3) 각 layer는 3차원 input volume을 미분 가능한 함수를 통해 3차원 출력 volume으로 변환시킨다.
4) Parameter가 있는 layer도 있고, 그렇지 않은 layer도 있다.
5) Hyper-parameter가 있는 layer도 있고, 그렇지 않은 layer도 있다.
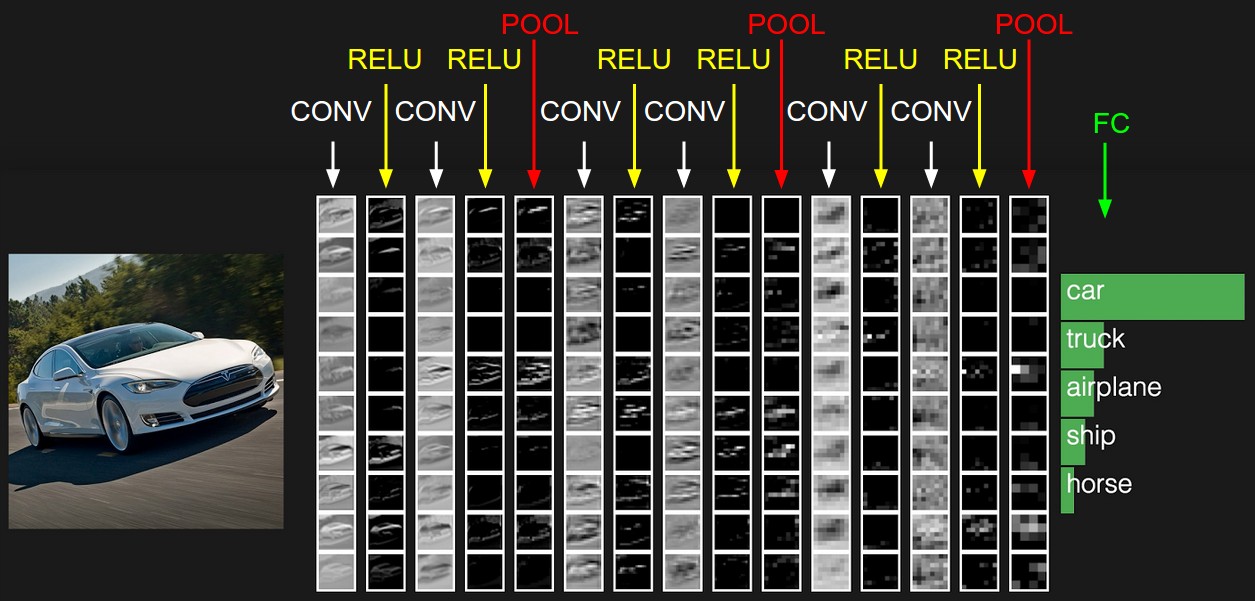
ConvNet의 architecture의 예제는 밑의 그림에서 잘 설명하고 있다.
Convolutional layer
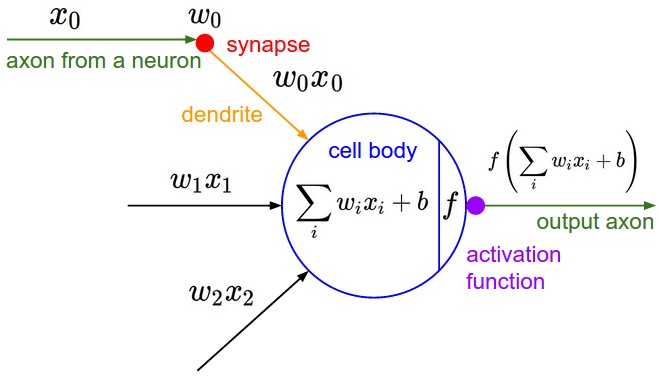
Conv layer의 parameter들은 일련의 학습가능한 filter들로 이루어져 있다. 각 filter는 width/height 차원으로는 작지만 depth 차원으로는 전체 깊이를 아우른다. Forward pass때에는 각 filter를 입력 volume의 width/height 차원으로 sliding시키며 (Convolution 연산) 2차원 activation map을 생성한다. Convolution 연산때, dot product가 진행된다. ConvNet은 입력의 특정 위치에 특정 pattern에 반응하는 (activate) filter를 학습한다. Activation map을 depth 차원을 따라 쌓은 것이 output volume이 된다. Output volume의 각 요소들은 input의 작은 영역 (local field)만을 취급하고, 같은 activation map의 neurons은 같은 parameter를 공유한다. (같은 필터를 적용한 결과) (하나의 filter당 하나의 activation map이 생성된다.)
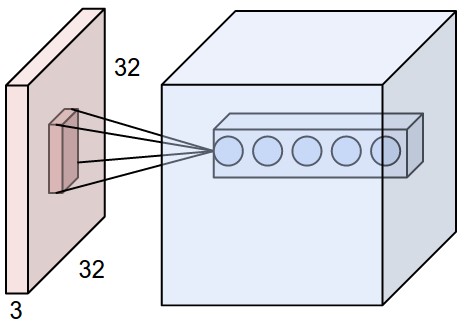
Image와 같은 고차원 (3차원) input을 다룰 때, 현재 layer의 한 neuron을 이전 volume의 모든 neuron과 연결시키는 것은 비 실용적이다 (fully connected neural network의 문제). 대신에, Convolutional layer는 input volume의 local region에만 연결을 한다. 이 영역은 receptive field라고 불린다.
예를 들어, [32 x 32 x 3]이 input volume이라면, receptive field의 크기가 5 x 5라면, convolutional layer는 5 x 5 x 3 = 75개의 weight을 갖게 된다. 만약 input volume이 [16 x 16 x 20]이라고 하자. 3 x 3 receptive field를 가즌다면 convolutional layer는 3 x 3 x 20 = 180개의 weight을 갖게 된다.
Convolutional layer에서 depth, stride 그리고 padding은 중요한 hyper-parameter이다.
1. Output volume의 depth는 결정하는 요소이다. Convolutional layer의 neurons 중 input volumne 내 동일한 영역과 연결된 neurons의 개수를 의미한다. 이런 점은 서로 다른 특징 (feature)에 activated된다. Image에서 input으로 받는 first convolutional layer의 경우, depth축에 따른 neurons은 이미지의 서로 다른 edge, color, blob등에 활성화 된다. (즉, 서로 다른 feature를 학습한다.) input의 서로 같은 영역을 바라보는 neuron들을 depth column이라고 부른다.
2. 두 번째로, stride를 결정해야한다. stride가 1이라면, 1칸마다 할당하게 된다. 이럴 경우, output volume의 크기도 매우 커지게 된다. 반대로 stride가 크다면, receptive field끼리 좁은 영역만 겹치게 되고, output volume도 작아지게 된다. (depth와는 상관이 없다.)
3. Input volume의 가장자리를 0으로 padding하는 것이 좋을 때가 있다. zero-padding은 hyper-parameter이다. zero-padding을 사용할 때, input volume의 크기가 유지되는 장점이 있다.
Output volume의 크기는 다음과 같이 정의된다.
W: input volume 크기
F : receptive field 크기
S : stride
P : zero-padding size
Convolutional layer의 weights은 filter또는 kernel이라고 불리며, convolution의 결과물은 activation map이 되며, 각 depth에 해당하는 filter의 activation map들을 쌓으면 최종 output volume이 된다.

위의 그림은 학습된 filter로, receptive field 11 x 11에 해당하는 weight을 보여주고 있다.
다음은 Convolution demo를 보여주고 있는데, convolutional layer의 연산을 정말 잘 설명해주고 있다.
Pooling layer
ConvNet 구조에 convolutional layer들 중간중간에 주기적으로 pooling layer를 넣는 것이 일반적이다. Pooling layer는 network의 parameter의 개수나 연산량을 줄이기 위해서 representation의 spatial size를 줄이는 것이다. Pooling layer는 또 over-fitting을 조절하는 효과를 갖고 있다.
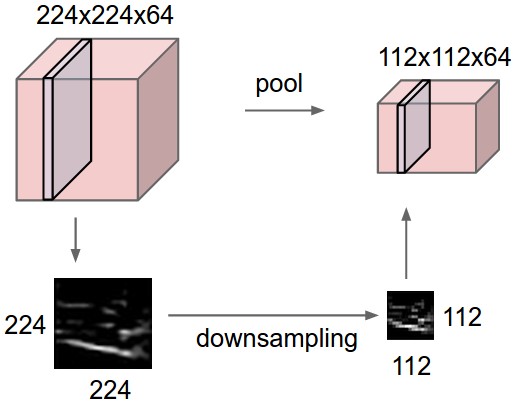
Pooling layer는 Max 연산을 각 depth slice에 대해 독립적으로 적응하여 spatial한 크기를 줄인다. size 2 x 2 stride 2가 가장 많이 사용되는 pooling layer이다. 각 depth slice는 width/height 축을 따라 1/2로 downsampling해 75 %의 activation은 버려진다. 단, depth 차원의 개수는 변하지 않는다.
Max pooling 뿐만 아니라, average pooing, L2-norm pooling등 다른 연산으로 pooling을 할 수 있다. 밑의 그림은 pooling 연산을 보여주고 있다.
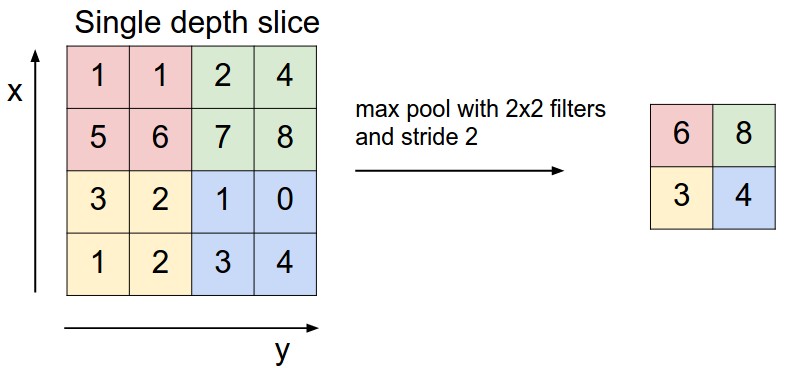
Backpropagation 에서 max(x,y)의 backward pass는 forward pass에서 가장 큰 값을 가졌던 입력의 gradient를 보내는 것과 같다. 따라서, forward pass과정에서 보통 max activation의 위치를 저장한다. (switch라고 한다. Deconvolutional neural networks에서 주로 사용된다.)
Pooling layer가 보통 representation의 크기를 심하게 줄이기 때문에 (이런 효과는 작은 데이터셋에서만 over-fitting 방지 효과 등으로 도움이 된다.) 최근 추세는 점점 pooling layer를 사용하지 않는 쪽으로 발전하고 있다.
Normalization layer
Fully-connected layer
이전 layer의 모든 activation들과 연결하여 class score를 계산한다. (Activation을 연결할 때, Flatten function을 사용해서 3D 구조를 1D로 변환시킨다.)
ConvNet architecture
"큰 receptive field를 가지는 conv layer를 하나 대신 여러 개의 작은 filter를 가진 conv layer를 쌓는 것이 좋다. 3 x 3 크기의 conv layer 3개를 쌓는다고 하면, 결국 7 x 7 영역을 보는 것과 같다. 따라서 여러 개의 작은 filter를 쌓는 것은 큰 receptive field를 갖는 conv layer와 동일하다. 하지만, 큰 receptive field를 사용하는 경우 단일 선형 함수를 적용할 뿐만 아니라, (3x3을 여러개 쌓고 non linear function을 사용한 경우가 비선형적인 feature를 더 고려할 수 있다.) parameter의 개수가 더 많음으로 문제가 생긴다. 따라서, 하나의 큰 filter를 갖는 convolution layer보다 작은 filter를 갖는 여러 개의 convolutional layer를 쌓는 것이 더 적은 parameter를 사용하면서도 입력으로부터 더 좋은 feature를 추출하는 것을 도와준다.
(이후 내용은 그렇게 중요하지 않아보여 skip을 한다. http://aikorea.org/cs231n/convolutional-networks/에서 100 % 번역하고 있으므로, 참고하길 바란다.)
'Deep learning study > CS231n' 카테고리의 다른 글
| Transfer Learning and Fine-tuning Convolutional Neural Networks (0) | 2019.03.02 |
|---|---|
| Understanding and Visualizing Convolutional Neural Networks (0) | 2019.03.02 |
| Neural Networks Part 3: Learning and Evaluation (0) | 2019.03.02 |
| Neural Networks Part 2: Setting up the Data and the Loss (0) | 2019.03.02 |
| Neural Networks Part 1: Setting up the Architecture (0) | 2019.03.01 |
