| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Machine Learning
- 기계학습
- 설명가능한 인공지능
- Class activation map
- 딥러닝
- cs231n
- Artificial Intelligence
- coding test
- Unsupervised learning
- Score-CAM
- 메타러닝
- 설명가능한
- AI
- 머신러닝
- keras
- xai
- grad-cam
- Deep learning
- meta-learning
- 백준
- 코딩 테스트
- Explainable AI
- Interpretability
- SmoothGrad
- python
- 코딩테스트
- Cam
- GAN
- 시계열 분석
- 인공지능
- Today
- Total
TestK
CV 5. Geometry 본문
Computer Vision [5]
1. Homography
동일한 물체에 대해서 다른 위치에서의 찍힌 두 이미지 사이의 관계는 구할 수 있을까? Homography는 아주 simple한 방법으로 이 관계를 설명할 수 있다.
두 이미지의 관계를 나타내기 위해서는 Homography matrix H를 통해 Mapping될 pair point들이 모두 같은 plane에 있어야한다는 제약이 있다. Homography를 estimation하는 과정을 깊게 파악해보자.
다음 두 점이 pair를 이룬다고 하자, (이때 중요한건 pair들이 collinear 하면 안된다. 즉, estimation하는데 사용되는 3개의 점들이 선 하나 위에 있으면 안된다.)
Homography Matrix H에 의해서 위와 같이 하나의 pair에서 두개의 eqution을 얻을 수 있으며, 이를 Matrix로 나타내면 다음과 같다.
총 9개의 parmaeter이지만, Homogeneous Coordinate System에서 Scale에 대해는 상관하지 않아도 되므로, Homography matrix H의 9개의 parameter중 8개만 estimation하면되고, 하나의 pair에서 2개의 equation을 얻을 수 있으니, 총 4개의 pair (No collinear)를 사용하면된다.

위와 같이 A와 h로 행렬과 벡터를 나타내면, 우리의 objective function은 다음과 같고, Least Square Method를 사용하면 답을 구할 수 있다.
Homography Matrix H를 추정하기 전에, A Matrix를 Normalize를 해줄 필요가 있는데, 이는 곱셈연산(x_i*x_i'와 같은)과 단순 x_i 사이의 scale이 다르기 때문이다. 다른 scale로 인해서 eigen decomposition을 구할 때 unstable한 성질을 갖게 되어 정확한 h를 추정하기가 어렵다. 따라서 "Isotropic Scaling Transform"을 해야한다. Points의 중심을 Origin으로, Origin에서 각 Point의 평균 거리가 2의 제곱근이 되도록 Scaling을 한다. (Scale Transformation)
따라서, 다음과 같이 최종적인 Homography Matrix H를 구할 수 있다.
T는 x_i의 scale transformation matrix, T'은 x_i`의 scale transformation matrix. hat이 붙어있는 H는 T와 T`로 transformed points들 사이의 추정된 Homography Matrix H를 가리킨다.
2. Epipolar Geometry
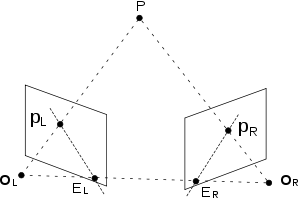

Example of epipolar geometry. This paragraph needs clarification as the content is not clear: if the two camera plane coincide[clarification needed] then the two epipoles are undetermined as intersection of one optical center of one camera with the other camera plane is not a point but a line. Two cameras, with their respective centers of projection points OL and OR, observe a point P. The projection of P onto each of the image planes is denoted pL and pR. Points EL and ER are the epipoles.
출처: Wikipedia, Epipolar geometry, https://en.wikipedia.org/wiki/Epipolar_geometry
두개의 카메라가 하나의 물체를 서로 다른 위치에서 찍고 있다고 가정해보자. 첫번째 카메라가 다른 카메라와 물체를 바라보는 "이미지"와 두번째 카메라가 첫번째 카메라와 물체를 바라보는 "이미지"사이에는 특정 관계가 있다. 정확히는 첫번째 카메라가 두번째 카메라를 보는 이미지 내에서의 point는 두번째 카메라가 첫번째 카메라를 보는 이미지 내에서의 line과 연관이 있다는 것이다. 이는 다음과 같이 표현된다.
E는 Essential Matrix라고 불리며, x는 첫번째 카메라의 view의 특정 물체가 projection되는 point이고, l'은 이에 해당하는 두번째 카메라의 view의 line 혹은 동일 물체가 두번째 카메라의 view에 projection되는 point candidates이다. (왜 candidates이냐면, 정확한 위치를 알 수 없기 때문이다.) 이 식은 다음과 같은 특징을 갖는데,
x'은 두번째 카메라 view의 특정 물체가 projection되는 point이다. 이 point는 "항상" point candiates 혹은 line l'위에 있으므로 0이 된다. 이 개념을 확장 시키면, 다음과 같은 부수적인 특징을 얻는다.
l은 두번째 카메라 view의 특정 물체가 projection되는 point x'에 대응되는 첫번째 카메라 view의 point candiates or line이다. e'는 두번째 카메라 view에 첫번째 카메라가 projection되는 point이고, e는 첫번째 카메라 view에 두번째 카메라가 projection되는 point이다. 이 관계는 쉽게 line위에 점이 있다면 그 점과 line 사이의 inner product는 0이된다는 점에서 쉽게 끌어낼 수 있다.
Camera의 Intrinsic parameter를 알고 있다면, Essential Matrix를 쓰지만, 사실 그렇지 않기 때문에 더 general한 개념인 Fundamental Matrix를 사용해야하며, 다음과 같이 표현된다.
K는 camera의 intrinsic parameter를 표현하는 matrix이다.
Fundamental Matrix은 3 x 3 matrix로 총 9개의 parameter를 estimation해야하지만, Homography와 마찬가지로 Homogeneous Coordinate System에서는 Scale에 대한 부분은 무시가 되므로, 총 8개의 parameter를 추정하면 되고, 다음 행렬 식으로 하나의 pair에 대해서 1개의 equation을 얻을 수 있다.
총 8개의 parameter를 추정해야하고, 하나의 pair에서 하나의 equation을 얻을 수 있으므로, 총 8개의 point가 필요하다.
Homography와 마찬가지로, 다른 scale로 인한 eigen decomposition의 unstability를 해결하기 위해서 scale transformation이 필요하다.
앞의 Least square methods를 풀면, 최적의 f를 구할 수 있지만, 여기서 마무리하면 안된다. Fundamental matrix와 Essential matrix는 full rank matrix가 아닌, rank가 2인 matrix이다. 반면에 위의 식을 푼 결과 얻은 f는 full rank(=3) 이므로, rank의 수를 다음과 같은 방법으로 줄인다.
3. RANSAC + Homography or Fundamental Matrix
RANSAC을 사용해서 Homography Matrix H혹은 Fundamental Matrixl F를 추정할 때, 가장 중요한 것은 inlier 혹은 outlier로 판단하기 위한 distance를 결정하는 방법이다. Google에서 찾아보면 다양한 방법이 있겠지만, 간단히 mapping된 point와 groundtruth point 사이의 distance가 a fixed threshold 미만이면 inlier로 그외는 outlier로 판단을 하여 RANSAC을 진행할 수 있다. 모델이야 H와 F가 그 역할을 해주며, s는 Homography Matrix H는 4가 될 것이고, Fundamental Matrix F는 8이 된다.
'Computer Vision > CV' 카테고리의 다른 글
| CV 7. Metric Learning (1) | 2018.12.26 |
|---|---|
| CV 6. Classification (0) | 2018.12.23 |
| CV 4. Camera Model (0) | 2018.12.22 |
| CV 3. Fitting (0) | 2018.12.21 |
| CV 2. SIFT (0) | 2018.12.21 |









