| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 설명가능한 인공지능
- grad-cam
- 백준
- coding test
- SmoothGrad
- AI
- GAN
- 시계열 분석
- 인공지능
- 코딩 테스트
- Interpretability
- 딥러닝
- Artificial Intelligence
- 메타러닝
- xai
- Cam
- 설명가능한
- Explainable AI
- 코딩테스트
- cs231n
- 머신러닝
- Class activation map
- meta-learning
- Machine Learning
- Deep learning
- Score-CAM
- python
- 기계학습
- Unsupervised learning
- keras
- Today
- Total
iMTE
CV 4. Camera Model 본문
Computer Vision [4]
1. Camera Model
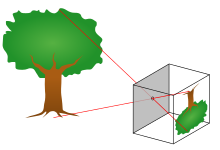
World의 물체는 Camera의 Lens를 통해 Sensor Plane에 투영이되고 우리는 이를 Image의 형태로 받아낸다. 따라서 Camera Model을 구하는 것은 실제 3D 물체의 coordinate와 Image의 coordinate의 관계를 찾는 것이다. 즉, I=MX, I는 2D Image이고 X는 3D 물체의 coordinate 그리고 M은 이 둘 사이의 관계인 "Camera Model"이다.
2. Homogeneous Coordinate
가장 먼저 이해해야할 내용은 Homogeneous Coordinate이다.
기본적인 coordinate system에서는 vector를 밑의 식과 같이 표현한다.
하지만, Homogeneous Coordinate에서는 다음과 같이 vector를 표현한다.
Homogeneous Coordinate의 vector 표현법은 두가지의 특징을 갖는다.
1) 3번째 성분이 1이되어서, [1,2,1] 과 [2,4,2]는 같은 vector로 취급된다.
2) 만약 w가 0인 경우 무한대 점을 가리킬 수 있다.
1)의 특징으로 인해서 Homogeneous Coordinate System은 Scale에 대한 별다른 정의를 하지 않아도 된다. 이로 인해서 이후에 보게 될 Homography의 parameter를 추정 할 때 Degree of Freedom이 줄어드는 효과를 얻게 된다.
3. 2D Transformations
1) Translation
위치를 수정하는 transformation 이다.
2) Euclidean
각도 및 위치를 수정하는 transformation 이다.
3) Scale
각도, 위치, 크기를 수정하는 transformation 이다.
4) Affine
Affine은 위의 1)~3) transformations을 포함하며, 더해서 Shear의 특성을 갖는다.
a11~a22는 A matrix로 표현되며, A matrix는 Non-singular 한 특징을 갖고 있어야한다. (Full rank, rank = 2) 이는 A가 singular matrix인 경우 mapping 되는 point가 중첩이 될 수 있기 때문이다.
5) Homography
Homography Matrix H는 h11~h33으로 표현되며, 1)~4) transformation과 달리 "Proportional"한 특징을 갖고 있음을 알 수 있다. 이는 1)~4) transformation은 3번째의 성분에 별다른 변화를 주지 않기 때문에 "="이지만, Homography는 3번째의 성분이 변화되고 Homogeneous Coordinate System으로 표현되기 위해서는 3번째 성분이 1이되는 변환이 추가적으로 필요하기 때문이다.
동일한 내용으로, Homography Matrix H에서 추정해야할 parameter는 8개인데 이는 Scale에 불변하기 때문이다. 만약, h33=1이어도, Homography Matrix H는 저 위의 식을 만족해야한다. h33이 2라도 H는 만족해야한다. 1과 2는 결국 특정 "기준 값"으로 볼 수 있으므로 9개중에서 1개의 parameter의 개수가 줄어들어 총 8개만 estimation하면 된다.
4. 3D Transformation
1) Rotation
x축이 기준이 되어 회전하는 Rx, y축이 기준이 되어 회전하는 Ry, z축이 기준이 되어 회전하는 Rz의 곱이 최종적인 "General Rotation"이 된다.
2) Projection
(1) Orthographic Projection
Orthographic Projection의 특징은 z값이 고려되지 않는 채로 Projection이 된다는 것이다.
(2) Perspective Projection
Perspective Projection은 (1)과 달리 z값이 고려된 것으로 z값에 따라 homogeneous coordinate vector로 바꿔줘야하므로 Scale에 따라 x,y값이 변화되므로 "="가 아닌 "Proportional" 관계가 된다.
5. Camera Model (Pinhole Model)
다양한 Camera Model을 고려할 수 있겠지만, 문제를 간단하게 만들기 위해서 Pinhole Model이 사용될 수 있다. 하나의 hole을 통해서만 빛이 전달이 되는 경우를 고려한 case로 thin-lens model의 ideal한 case이다.
Pinhole Model은 다음과 같이 표현된다.
[u,v,1]은 Image Coordinate의 Homogeneous Coordinate system의 vector이며, K는 Camera의 Intrinsic parameter를 표현하는 Matrix이다. [x,y,z,1]은 World Coordinate의 vector이다. 따라서, Pinhole Model은 World Coordinate로 부터 3D transformation을 거친 이후에 2D 평면에 Perspective Projection을 진행하고 Camera Intrinsic Parameter Matrix로 보정하는 과정을 포함하는 "관계"다.
K는 Camera의 Intrinsic Parameter Matrix로서, f는 aspect ratio을 의미하며, 밑 첨자 x,y는 축방향을 의미한다. s는 skew parameter를 u0와 v0는 optical center를 의미한다. r11~r33은 Camera의 Rotation을 의미한다.
K[R,t]를 M으로 바꾸면, 4차원의 vector를 3차원의 vector를 mapping하는 Matrix가 된다. 3차원의 vector와 4차원사이의 (정확히 말하면 2차원과 3차원 사이의) Pair를 바탕으로 M(3 x 4)의 parameter를 Least Square Method를 사용하여 추정할 수 있으며, 만약 Pair에 outlier가 있다면, RANSAC을 사용하면 M을 구할 수 있다. 계산된 M을 갖고, K와 t에 대한 값을 계산할 수 있다.
'Computer Vision > CV' 카테고리의 다른 글
| CV 6. Classification (0) | 2018.12.23 |
|---|---|
| CV 5. Geometry (0) | 2018.12.23 |
| CV 3. Fitting (0) | 2018.12.21 |
| CV 2. SIFT (0) | 2018.12.21 |
| CV 1. Local Features (2) | 2018.12.21 |